Regularized Cox Regression
Kenneth Tay
Noah Simon
Jerome Friedman
Trevor Hastie
Rob Tibshirani
Balasubramanian Narasimhan
March 27, 2023
Coxnet.RmdIntroduction
This vignette describes how one can use the glmnet package to fit regularized Cox models.
The Cox proportional hazards model is commonly used for the study of the relationship beteween predictor variables and survival time. In the usual survival analysis framework, we have data of the form \((y_1, x_1, \delta_1), \ldots, (y_n, x_n, \delta_n)\) where \(y_i\), the observed time, is a time of failure if \(\delta_i\) is 1 or a right-censored time if \(\delta_i\) is 0. We also let \(t_1 < t_2 < \ldots < t_m\) be the increasing list of unique failure times, and let \(j(i)\) denote the index of the observation failing at time \(t_i\).
The Cox model assumes a semi-parametric form for the hazard \[ h_i(t) = h_0(t) e^{x_i^T \beta}, \] where \(h_i(t)\) is the hazard for patient \(i\) at time \(t\), \(h_0(t)\) is a shared baseline hazard, and \(\beta\) is a fixed, length \(p\) vector. In the classic setting \(n \geq p\), inference is made via the partial likelihood \[ L(\beta) = \prod_{i=1}^m \frac{e^{x_{j(i)}^T \beta}}{\sum_{j \in R_i} e^{x_j^T \beta}}, \] where \(R_i\) is the set of indices \(j\) with \(y_j \geq t_i\) (those at risk at time \(t_i\)).
Note there is no intercept in the Cox model as it is built into the baseline hazard, and like it, would cancel in the partial likelihood.
In glmnet, we penalize the negative log of the partial likelihood with an elastic net penalty.
(Credits: The original "coxnet" algorithm for right-censored data was developed by Noah Simon, Jerome Friedman, Trevor Hastie and Rob Tibshirani: see Simon et al. (2011) for details. The other features for Cox models, introduced in v4.1, were developed by Kenneth Tay, Trevor Hastie, Balasubramanian Narasimhan and Rob Tibshirani.)
Basic usage for right-censored data
We use a pre-generated set of sample data and response. x must be an \(n\times p\) matrix of covariate values — each row corresponds to a patient and each column a covariate. y is an \(n \times 2\) matrix, with a column "time" of failure/censoring times, and "status" a 0/1 indicator, with 1 meaning the time is a failure time, and 0 a censoring time. The Surv function in the survival package creates such a response matrix, and it is recommended that the user uses the output of a call to Surv for the response to glmnet. (For backward compatibility, glmnet can accept a two-column matrix with column names "time" and "status" for right-censored data.)
## Loading required package: Matrix## Loaded glmnet 4.1-7## time status
## [1,] 1.76877757 1
## [2,] 0.54528404 1
## [3,] 0.04485918 0
## [4,] 0.85032298 0
## [5,] 0.61488426 1We apply the glmnet function to compute the solution path under default settings:
fit <- glmnet(x, y, family = "cox")All the standard options such as alpha, weights, nlambda and standardize package, and their usage is similar as in the Gaussian case. (See the vignette “An Introduction to glmnet” for details, or refer to the help file help(glmnet).)
We can plot the coefficients with the plot method:
plot(fit)
As before, we can extract the coefficients at certain values of \(\lambda\):
coef(fit, s = 0.05)## 30 x 1 sparse Matrix of class "dgCMatrix"
## 1
## V1 0.37693638
## V2 -0.09547797
## V3 -0.13595972
## V4 0.09814146
## V5 -0.11437545
## V6 -0.38898545
## V7 0.24291400
## V8 0.03647596
....Since the Cox Model is not commonly used for prediction, we do not give an illustrative example on prediction. If needed, users can refer to the help file by typing help(predict.glmnet).
Cross-validation
The function cv.glmnet can be used to compute \(K\)-fold cross-validation (CV) for the Cox model. The usage is similar to that for other families except for two main differences.
First, type.measure only supports "deviance" (also default) which gives the partial-likelihood, and "C", which gives the Harrell C index. This is like the area under the curve (AUC) measure of concordance for survival data, but only considers comparable pairs. Pure concordance would record the fraction of pairs for which the order of the death times agree with the order of the predicted risk. However, with survival data, if an observation is right censored at a time before another observation’s death time, they are not comparable.
The code below illustrates how one can perform cross-validation using the Harell C index. Note that unlike most error measures, a higher C index means better prediction performance.
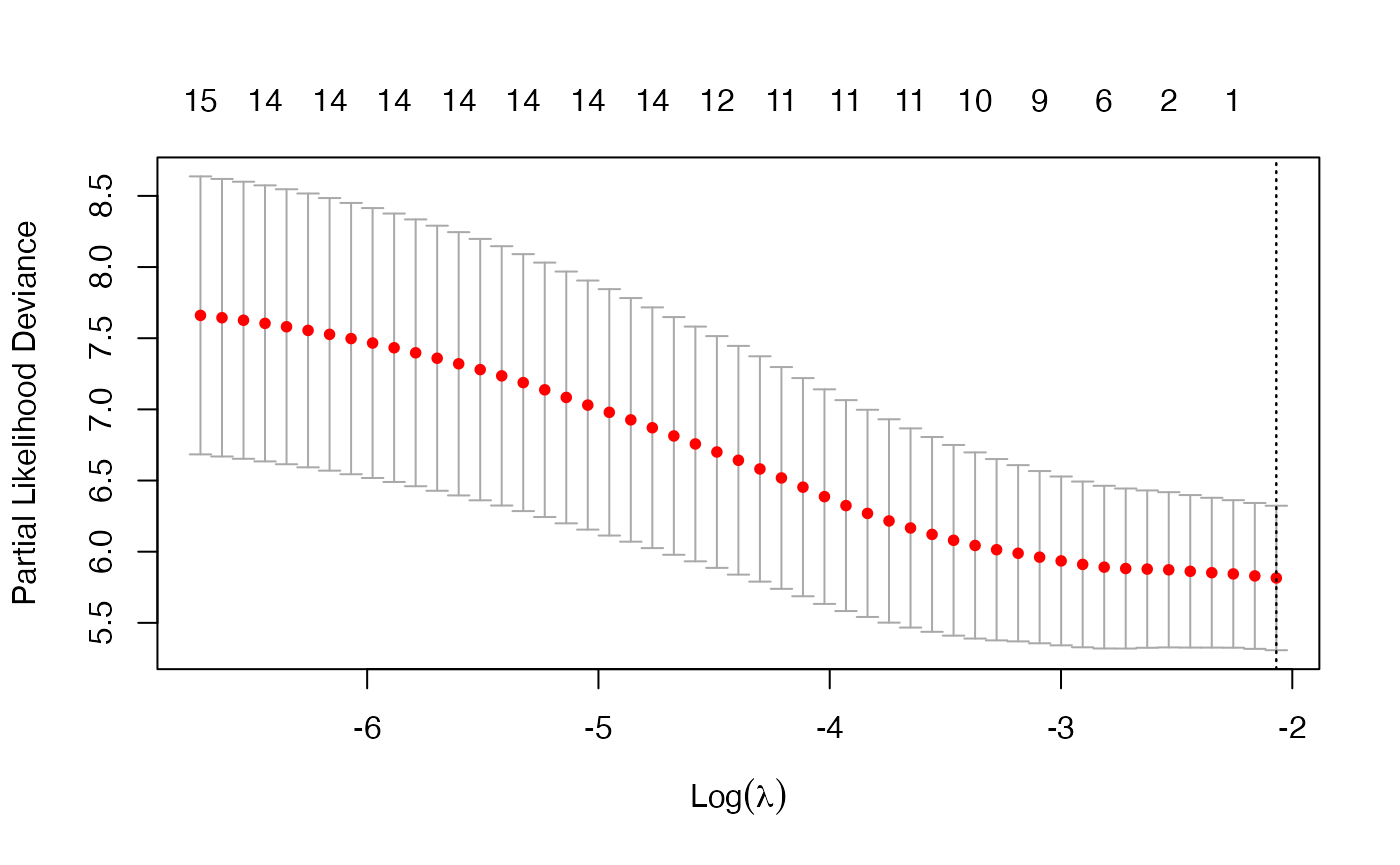
Once fit, we can view the optimal \(\lambda\) value and a cross validated error plot to help evaluate our model.
plot(cvfit)
As with other families, the left vertical line in our plot shows us where the CV-error curve hits its minimum. The right vertical line shows us the most regularized model with CV-error within 1 standard deviation of the minimum. We also extract such optimal \(\lambda\)’s:
cvfit$lambda.min## [1] 0.03057865
cvfit$lambda.1se## [1] 0.05864711Second, the option grouped = TRUE (default) obtains the CV partial likelihood for the Kth fold by subtraction, i.e. by subtracting the log partial likelihood evaluated on the full dataset from that evaluated on the \((K-1)/K\) dataset. This makes more efficient use of risk sets. With grouped = FALSE the log partial likelihood is computed only on the \(K\)th fold, which is only reasonable if each fold has a large number of observations.
Handling of ties
glmnet handles ties in survival time with the Breslow approximation. This is different from survival package’s coxph function, whose default tie-handling method is the Efron approximation.
# create x matrix
set.seed(1)
nobs <- 100; nvars <- 15
x <- matrix(rnorm(nobs * nvars), nrow = nobs)
# create response
ty <- rep(rexp(nobs / 5), each = 5)
tcens <- rbinom(n = nobs, prob = 0.3, size = 1)
y <- Surv(ty, tcens)
# coefficients from these two models will not line up because
# of different tie handling methods
glmnet_fit <- glmnet(x, y, family = "cox", lambda = 0)
coxph_fit <- coxph(y ~ x)
plot(coef(glmnet_fit), coef(coxph_fit))
abline(0, 1)
glmnet is not able to perform the Efron approximation at the moment. survival’s coxph can perform the Breslow approximation by specifying ties = "breslow":
# coefficients from these two models will line up
glmnet_fit <- glmnet(x, y, family = "cox", lambda = 0)
coxph_fit <- coxph(y ~ x, ties = "breslow")
plot(coef(glmnet_fit), coef(coxph_fit))
abline(0, 1)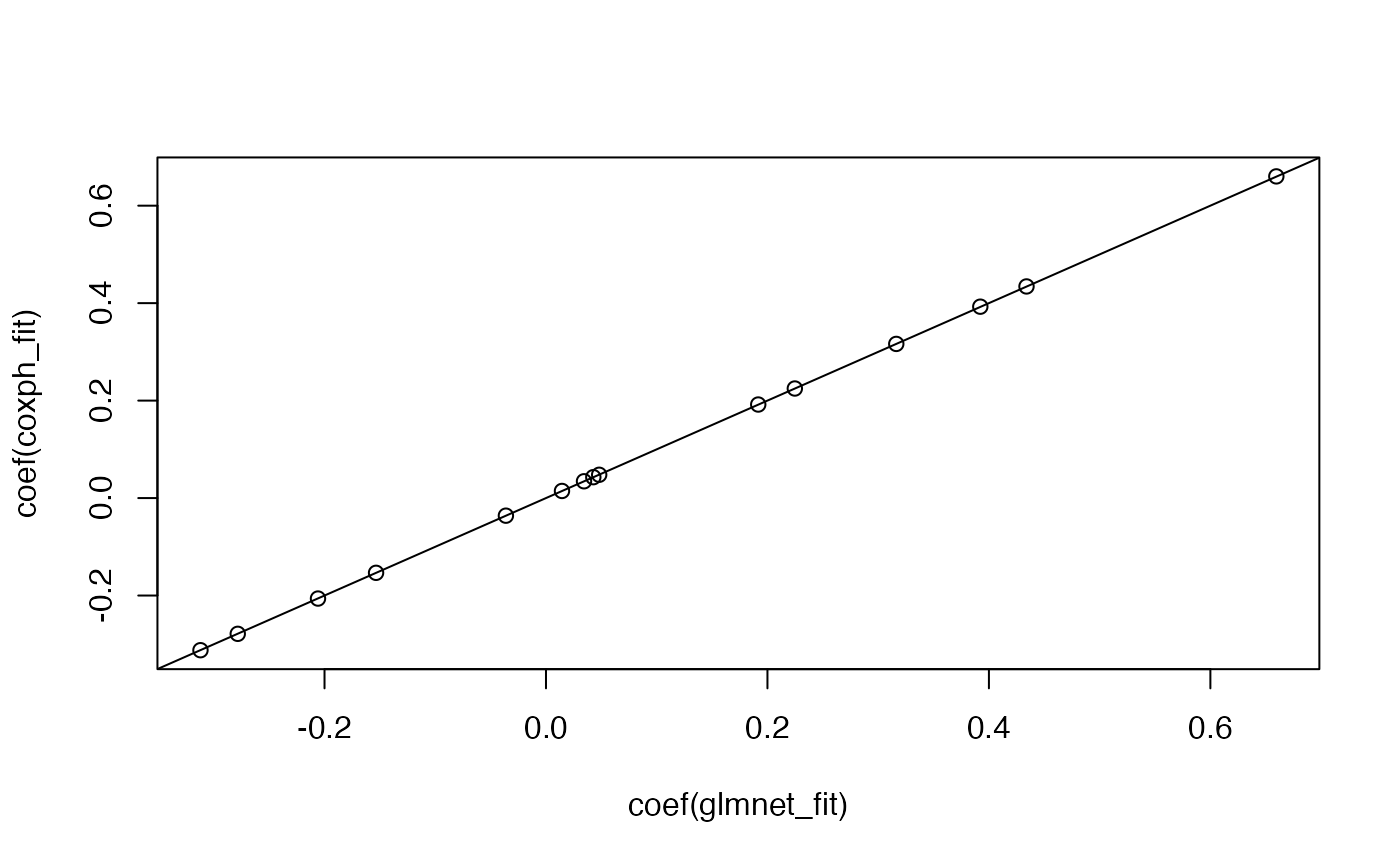
Cox models for start-stop data
Since version 4.1 glmnet can fit models where the response is a (start, stop] time interval. As explained in Therneau and Grambsch (2000), the ability to work with start-stop responses opens the door to fitting regularized Cox models with
- time-dependent covariates,
- time-dependent strata,
- left truncation,
- multiple time scales,
- multiple events per subject,
- independent increment, marginal, and conditional models for correlated data, and
- various forms of case-cohort models.
The code below shows how to create a response of this type (using survival package’s Surv function) and how to fit such a model with glmnet.
# create x matrix
set.seed(2)
nobs <- 100; nvars <- 15
xvec <- rnorm(nobs * nvars)
xvec[sample.int(nobs * nvars, size = 0.4 * nobs * nvars)] <- 0
x <- matrix(xvec, nrow = nobs) # non-sparse x
x_sparse <- Matrix::Matrix(xvec, nrow = nobs, sparse = TRUE) # sparse x
# create start-stop data response
beta <- rnorm(5)
fx <- x_sparse[, 1:5] %*% beta / 3
ty <- rexp(nobs, drop(exp(fx)))
tcens <- rbinom(n = nobs, prob = 0.3, size = 1)
starty <- runif(nobs)
yss <- Surv(starty, starty + ty, tcens)
# fit regularized Cox model with start-stop data
fit <- glmnet(x, yss, family = "cox")(Note that the call above would have worked as well if x was replaced by x_sparse.) cv.glmnet works with start-stop data too:

As a sanity check, the code below shows that fitting start-stop responses using glmnet with lambda = 0 matches up with coxph’s result:
glmnet_fit <- glmnet(x, yss, family = "cox", lambda = 0)
coxph_fit <- coxph(yss ~ x)
plot(coef(glmnet_fit), coef(coxph_fit))
abline(0, 1)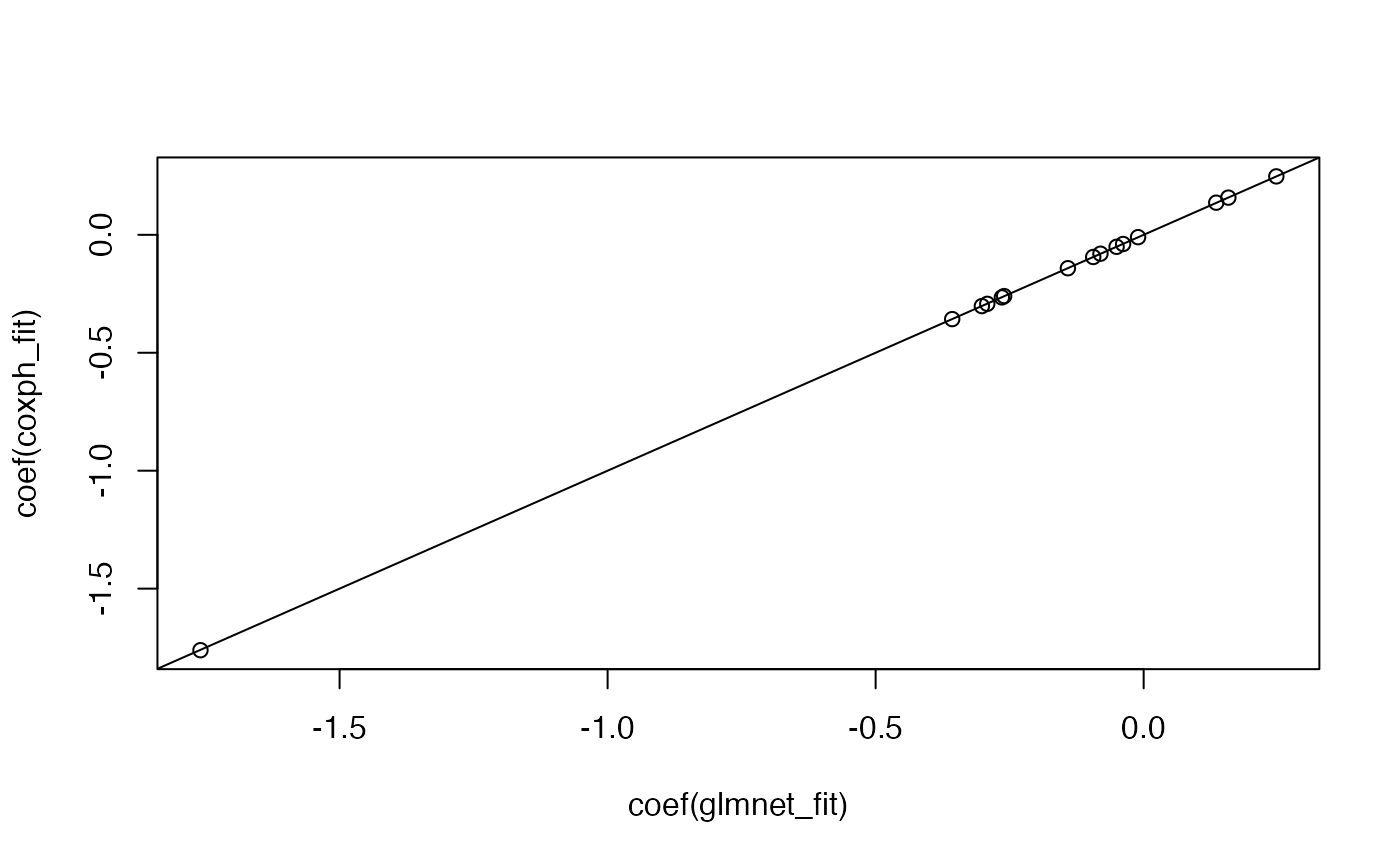
Stratified Cox models
One extension of the Cox regression model is to allow for strata that divide the observations into disjoint groups. Each group has its own baseline hazard function, but the groups share the same coefficient vector for the covariates provided by the design matrix x.
glmnet can fit stratified Cox models with the elastic net penalty. With coxph one can specify strata in the model formula. Since glmnet does not use a model formula, we achieve this by adding a strata attribute to the Surv response object. We achieve this via the function stratifySurv:
strata <- rep(1:5, length.out = nobs)
y2 <- stratifySurv(y, strata)
str(y2[1:6])## 'stratifySurv' num [1:6, 1:2] 0.605+ 0.605+ 0.605+ 0.605+ 0.605+ 0.816
## - attr(*, "dimnames")=List of 2
## ..$ : NULL
## ..$ : chr [1:2] "time" "status"
## - attr(*, "type")= chr "right"
## - attr(*, "strata")= int [1:6] 1 2 3 4 5 1stratifySurv returns an object of class stratifySurv. We can then pass this stratifySurv object as the response to a glmnet call. glmnet will fit a stratified Cox model if it detects that the response has class stratifySurv.
fit <- glmnet(x, y2, family = "cox")This stratifySurv object can also be passed to cv.glmnet to fit stratified Cox models with cross-validation:
Note that simply giving the response a "strata" attribute is not enough! The response needs to be of class stratifySurv in order for subsetting to work correctly. To protect against this, an error will be thrown if the response has a "strata" attribute but is not of class stratifySurv. Add strata via the stratifySurv function.
y3 <- y
attr(y3, "strata") <- strata
str(y3[1:6]) # note that the strata attribute is no longer there## 'Surv' num [1:6, 1:2] 0.605+ 0.605+ 0.605+ 0.605+ 0.605+ 0.816
## - attr(*, "dimnames")=List of 2
## ..$ : NULL
## ..$ : chr [1:2] "time" "status"
## - attr(*, "type")= chr "right"
fit <- glmnet(x, y3, family = "cox")## Error in use.cox.path(x, y): For fitting stratified Cox models, y must be of class stratifySurv, see ?stratifySurv for more detailsPlotting survival curves
Fitting a regularized Cox model using glmnet with family = "cox" returns an object of class "coxnet". Class "coxnet" objects have a survfit method which allows the user to visualize the survival curves from the model. In addition to the "coxnet" object, the user must pass the x and y objects used to fit the model (for computation of the baseline hazard), as well as the lambda value for which the survival curve is desired:
## Call: survfit.coxnet(formula = fit, s = 0.05, x = x, y = y)
##
## n events median
## [1,] 100 33 1.6We are unable to provide standard errors for these survival curves, so we do not present the confidence bounds for them. To plot the survival curve, pass the result of the survfit call to plot:
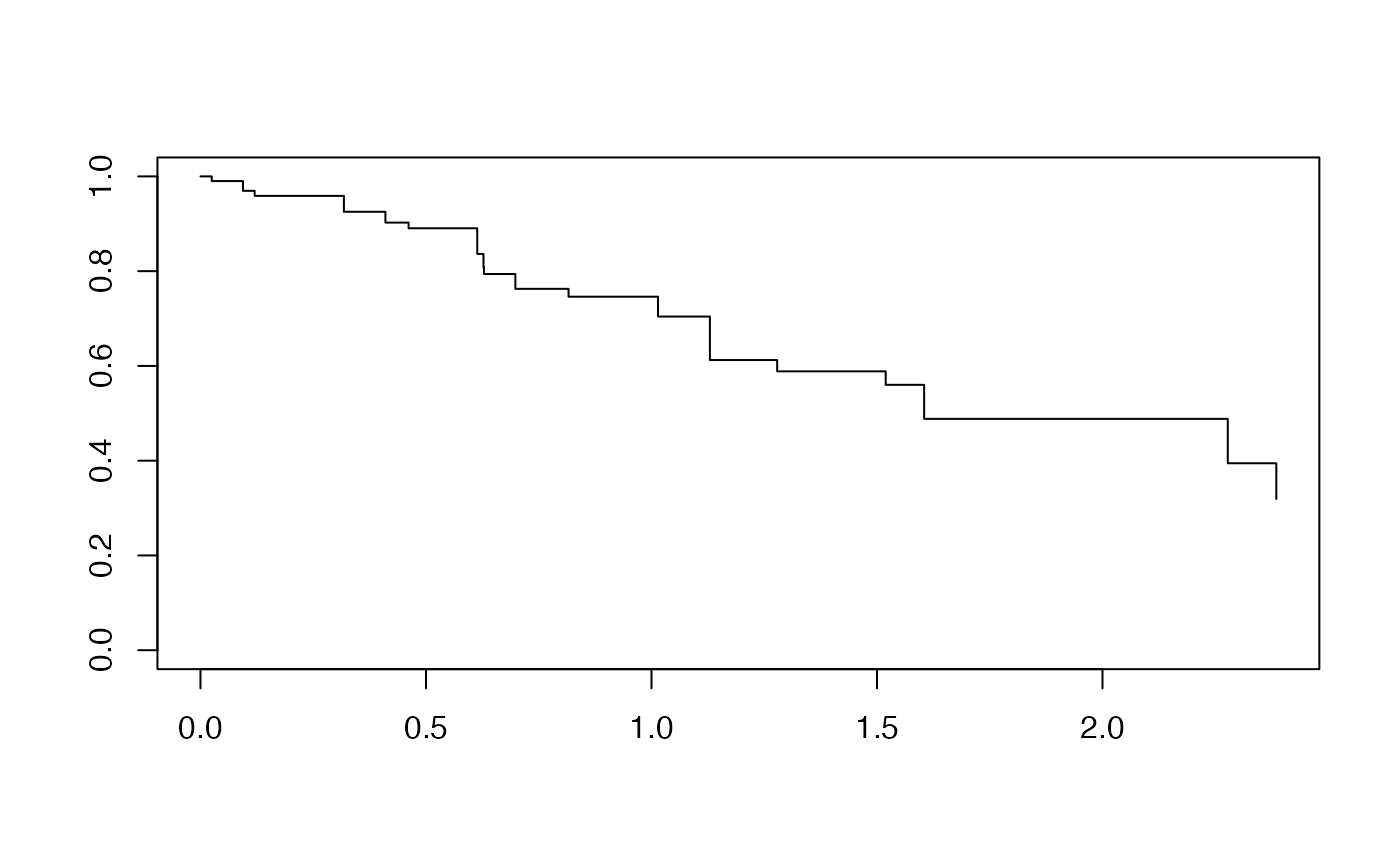
As noted in the documentation for survival::survfit.coxph, without new data, a curve is produced for a single “pseudo” subject with covariate values equal to the means of the data set, and this resulting curve(s) almost never make sense. We can get survival curves for individual observations by passing a newx argument:
survival::survfit(fit, s = 0.05, x = x, y = y, newx = x[1:3, ])## Call: survfit.coxnet(formula = fit, s = 0.05, x = x, y = y, newx = x[1:3,
## ])
##
## n events median
## 1 100 33 1.60
## 2 100 33 1.60
## 3 100 33 2.28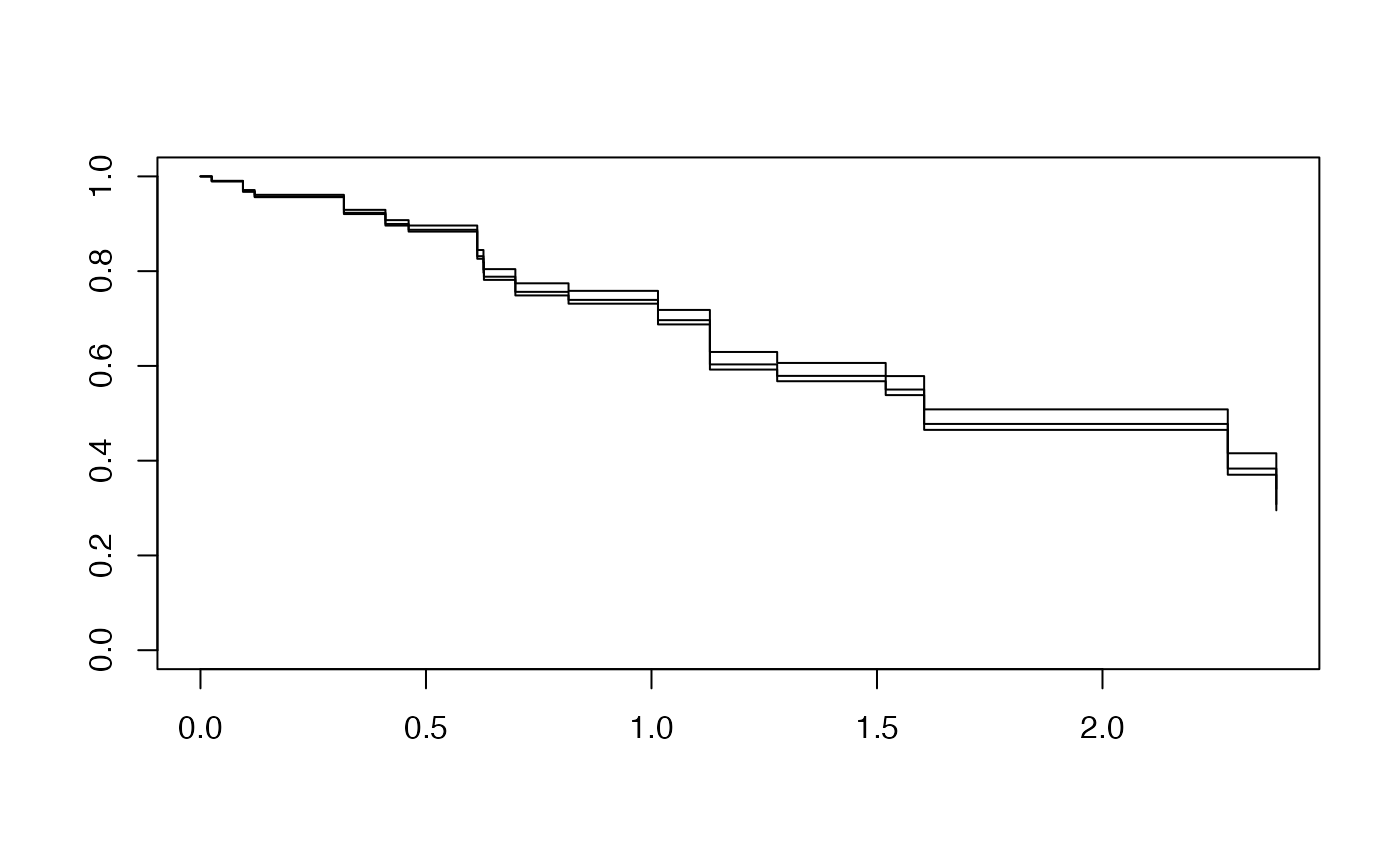
If the original model was fit with strata, then the strata option needs to be specified as well. If newx is being passed for such a model, the strata for these new observations need to be passed via newstrata.
y2 <- stratifySurv(y, rep(1:2, length.out = nobs))
fit <- glmnet(x, y2, family = "cox")
survival::survfit(fit, s = 0.01, x = x, y = y2)## Call: survfit.coxnet(formula = fit, s = 0.01, x = x, y = y2)
##
## n events median
## strata=1 50 18 1.52
## strata=2 50 15 2.28
# survival curve plot for first two individuals in dataset
plot(survival::survfit(fit, s = 0.01, x = x, y = y2,
newx = x[1:2, ], newstrata = strata[1:2]))
To be consistent with other methods in glmnet, if the s parameter is not specified, survival curves are returned for the entire lambda sequence. The survival curves are returned as a list, one element for each lambda value.
## [1] 48
length(fit$lambda)## [1] 48The survfit method is available for cv.glmnet objects as well. By default, the s value chosen is the “lambda.1se” value stored in the CV object. The s value can also be set to the "lambda.min" value stored in the CV object.
## Call: survfit.cv.glmnet(formula = cv.fit, x = x, y = y2)
##
## n events median
## strata=1 50 18 1.52
## strata=2 50 15 2.28
survival::survfit(cv.fit, s = "lambda.min", x = x, y = y2)## Call: survfit.cv.glmnet(formula = cv.fit, s = "lambda.min", x = x,
## y = y2)
##
## n events median
## strata=1 50 18 1.52
## strata=2 50 15 2.28References
Simon, Noah, Jerome Friedman, Trevor Hastie, and Robert Tibshirani. 2011. “Regularization Paths for Cox’s Proportional Hazards Model via Coordinate Descent.” Journal of Statistical Software, Articles 39 (5): 1–13. https://doi.org/10.18637/jss.v039.i05.
Therneau, Terry M., and Patricia M. Grambsch. 2000. Modeling survival data: extending the Cox model. Springer.